A few days ago I was poking around my alma mater’s website (Go Panthers!) and came across this math walk:
unimathwalk
(This math walk was originally posted at: http://www.uni.edu/math/sites/default/files/pdfs/unimathwalk.pdf )
I thought it was such a cool idea that I wanted to create a math walk of my own! (So I did).
I know that not all of you will be walking around Iowa City or The University of Iowa’s campus, so I thought I’d bring the math walk to you. I’d encourage you to:
1. Try my virtual math walk
and then . . .
2. Get some friends, or a class, or your family and create a math walk of your own. When you do, send it to me (katherine-degner@uiowa.edu) and I’ll post the math walks on my blog. Soon no one will be able to walk around without “thinking math.” Wouldn’t that be great!
My University of Iowa/Iowa City Math Walk
I work at the Belin-Blank Center, on the University of Iowa Campus . . . which is here:
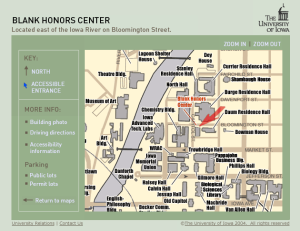
So, I headed out of the building toward the Pentacrest (more on that later) and the Old Capital.

I got no more than half a block when I ran in to this!
![photo[6]](https://katedegner.wordpress.com/wp-content/uploads/2013/09/photo6.jpg?w=225&h=300)
The official name of the sculpture is “Ridge and Furrow,” although many people at the University of Iowa refer to it as the “brain sculpture.” (For obvious reasons!). It was carved by artist Peter Randall-Page. The artist says that it is many up of one, continuous ridge flanked by v-shaped furrows.
1. The description made me think of the mobius strip. In other words, think of this as one great big twisty infinity symbol (which is a mobius strip, just FYI). I’m also wondering if we could cut the continuous ridge and stretch it out into a straight line, how long would it be? How could you estimate this?
As I headed toward the Pentacrest, I couldn’t help but notice the bricks I was walking on.
They looked like this. I also noticed they tessellated the plane.

2. Which made me wonder, how many other ways could I arrange these standard sized bricks so that they would continue to tessellate the plane? And, what wallpaper pattern does this tessellation belong to? Which really asks, “What type of symmetry is being used to create this pattern?”
In the middle of my math walk many classes let out and I was flooded by students. And I saw these two:

3. Which made me wonder, what are the chances of that happening? (In case you can’t tell from the picture, the two men are dressed exactly.the.same. blue t-shirts, khaki shorts). This question takes the form of “if you have 3 pairs of blue socks, and 2 pairs of green socks, what are the chances that . . .”
I was headed to the Pentacrest because I knew about a secret on the Pentacrest. I thought I was the only one that knew, until I found this. Anyway, “what’s the secret?” you might ask. Well, the University of Iowa Pentacrest is home to the largest walnut tree in the state of Iowa! Here it is:

This leads me to my next (maybe obvious? question).
4. How tall is the tree and how in the world do you measure it?
As promised at the beginning of the post, I have a little bit more to tell you about the Pentacrest. First, you may or may not know that penta- means 5. This might lead you to believe that the Pentacrest has five buildings. And if that’s where your thoughts lead you, you’d be right! The Pentacrest is a little piece of lawn which houses 5 university buildings (one of which is the Old Capitol). I tried to take a picture of the Pentacrest, but the truth is the professional photographers, that took ariel pictures just do a much better job. See:

Do you also see how it kind of looks like a pentagon? No, not THE Pentagon (which is a regular pentagon), but it does kind of look like a pentagon, except that the Old Capital isn’t a vertex. Anyway, this leads me to my last question on my math walk:
5. Is there a way to get to each of the 5 buildings using the sidewalks provided, such that I go to all buildings and walk on each sidewalk exactly once? (Kind of reminds you of the Bridges of Konigsberg Problem, doesn’t it?)
Whew! You made it! Happy math walking!
P.S. Once I started “math walking” I just couldn’t stop, so I snapped these pictures as I was walking home from work:


I’m wondering:
6. What percent of the house is covered in ivy?
7. Is that an equilateral triangle? How could we find out?








![photo[3]](https://katedegner.wordpress.com/wp-content/uploads/2014/01/photo3.jpg?w=300&h=225)





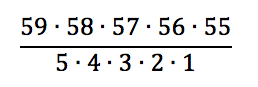


![photo[6]](https://katedegner.wordpress.com/wp-content/uploads/2013/09/photo6.jpg?w=225&h=300)





